Description

Let $L>0$ be the domain size and $m$ be a mollification parameter. Let $\tau\in C_{c}^{\infty}(\mathbb{R}^{2},[0,1])$ be even such that $\tau\equiv1$ in a neighbourhood of $0$. We define a mollified white noise with Neumann boundary conditions by \begin{equation*} \xi_{m}=\sum_{k\in\mathbb{N}_{0}^{2}}\tau((mL)^{-1}k)\mathscr{W}(\mathfrak{n}_{k})\mathfrak{n}_{k}, \end{equation*} where $\mathscr{W}$ denotes a (spatial) white noise and $(\mathfrak{n}_{k})_{k\in\mathbb{N}_{0}^{2}}$ an orthonormal basis of cosines.

The (Dirichlet) parabolic Anderson model on $(0,L)^{2}$ needs to be renormalized by a sequence of counter-terms $(c_{m})_{m\in\mathbb{N}}$ such that $c_{m}=\frac{1}{2\pi}\log(m)+c_{\tau}$, where $c_{\tau}$ depends only on $\tau$. With this sequence of counter-terms, it follows that the solutions to the mollified (Dirichlet) parabolic Anderson model \begin{equation*} (\partial_{t}-\Delta)u_{m}=(\xi_{m}-c_{m})u_{m} \end{equation*} converge as $m\to\infty$.

How does the renormalization affect an underlying population? Let $(X^{m})_{m\in\mathbb{N}}$ be a (killed) super Brownian motion in a mollified white-noise environment, that is, for every $\phi\in C_{0}((0,L)^{2})$ with $\Delta\phi\in C_{0}((0,L)^{2})$, it follows that \begin{equation*} \langle\phi,X^{m}_{t}\rangle-\langle\phi,X^{m}_{0}\rangle-\int_{0}^{t}\langle(\Delta+\xi_{m}-c_{m})\phi,X^{m}_{s}\rangle\mathrm{d}s \end{equation*} is a continuous, square-integrable martingale with quadratic variation \begin{equation*} \int_{0}^{t}\langle\phi^{2},X^{m}_{s}\rangle\mathrm{d}s. \end{equation*}

Let $T^{m}\phi$ denote the solution of the mollified parabolic Anderson model with initial data $\phi$. We can then identify linear moments of $X^{m}$: \begin{equation*} \mathbb{E}(\langle\phi,X^{m}_{t}\rangle)=\mathbb{E}(\langle T^{m}_{t}\phi,X^{m}_{0}\rangle). \end{equation*} Hence, to find a natural interpretation for the renormalization of the parabolic Anderson model, it suffices to find an individual-based model for the (killed) super Brownian motion in a mollified white-noise environment. A natural choice is a branching Brownian motion in an environment determined by mollified white noise.

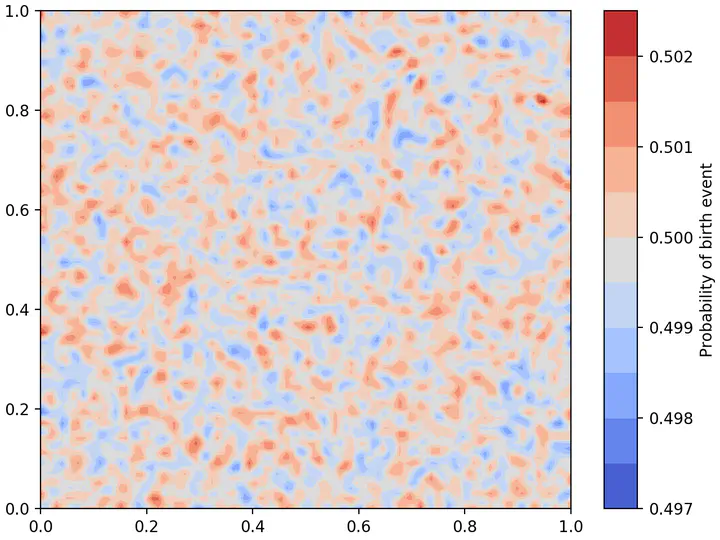
Fix a finite population size $n$. We define for $x\in(0,L)^{2}$, \begin{equation*} \zeta_{n,m}^{+1}(x)=\frac{1}{2}\Big(1+\frac{\xi_{m}(x)-c_{m}}{n}\Big),\quad\zeta_{n,m}^{-1}(x)=\frac{1}{2}\Big(1-\frac{\xi_{m}(x)-c_{m}}{n}\Big). \end{equation*} It follows that $\zeta_{n,m}^{+1}(x)+\zeta_{n,m}^{-1}(x)=1$ and, for $m$ sufficiently large, that $\zeta_{n,m}^{+1}(x),\zeta_{n,m}^{-1}(x)\in[0,1]$ uniformly in $x\in(0,L)^{2}$. Hence, we can interpret those quantities as probabilities.

Let $Y^{n,m}$ be a branching Brownian motion such that:

• particles evolve as variance- $2/n$-Brownian motions until they are killed upon reaching $\partial(0,L)^{2}$;
• branching events occur with rate $1$ at which a particle at position $x\in(0,L)^{2}$ either gives birth with probability $\zeta_{n,m}^{+1}(x)$ or dies with probability $\zeta_{n,m}^{-1}(x)$;
• particles are born at the location $x$ of their parent and evolve independently of them.

It then follows that $X^{n,m}_{t}=\frac{1}{n}Y^{n,m}_{nt}$ converges in distribution as $n\to\infty$ to $X^{m}_{t}$, the killed super Brownian motion in a mollified white-noise environment. Hence, the renormalization $(c_{m})_{m\in\mathbb{N}}$ affects the underlying particle dynamics through the branching probabilities $\zeta_{n,m}^{+1}(x),\zeta_{n,m}^{-1}(x)$ by introducing an asymptotically small perturbation of order $\log(m)/m$.

Highlights

• Identified an intermediate process, the killed mollified super Brownian motion, in the universality class of N. Perkowski and T. Rosati’s killed rough super Brownian motion [T.C. Rosati, N. Perkowski, Ann. Probab. 49(2), 2021; T.C. Rosati, Electron. Commun. Probab. 25, 2020]

• Developed a novel construction of singular stochastic PDEs with multiplicative noise and quadratic reaction terms based on Wild sums